Oggi parleremo di campionamento e quantizzazione audio;
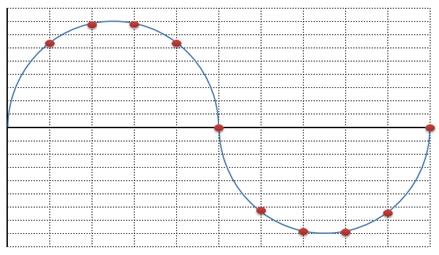
prendiamo un segnale semplice (un’onda sinusoidale – sine wave – a frequenza e ampiezza fisse) che supponiamo compia il suo ciclo in un secondo esatto (un’onda quindi con frequenza pari ad 1 Hz – inudibile all’essere umano, ma tanto utile per schematizzare il nostro lavoro) e immaginiamo di campionarla a una frequenza di 10 Hz (la nostra frequenza di campionamento sarà, manco a dirlo, pari a 10 Hz). Le linee tratteggiate verticali evidenziamo gli istanti in cui l’onda sarà campionata mentre il valore di tensione (asse Y) rilevato, evidenziato dai pallini rossi, è quello che sarà mantenuto costante nel circuito di hold per ogni frazione di secondo.
E ora viene il bello. Questo valore di tensione, un valore analogico e quindi continuo nei valori che può assumere, deve essere trasformato in valore digitale, usufruibile da parte del nostro calcolatore e quindi espresso con un numero binario. I valori a disposizione non sono infiniti e infatti le non infinite capacità di calcolo delle nostre macchine impongono un limite al numero di valori possibili che possiamo assegnare. Introduciamo il concetto di risoluzione (“bit depth”, in inglese), ovvero il numero di bit che il sistema mette a disposizione per descrivere il valore di ogni campione all’interno del nostro circuito di campionamento.
Sarebbe interessante (anche se non per tutti, mi rendo conto) una bella lezioncina di aritmetica binaria, ma direi che non è esattamente il nostro obiettivo, quindi saltiamo tutti i preliminari (applausi a scena aperta…) e prendiamo per partito preso quanto espresso nella tabella seguente.
L’interpretazione è semplice: il numero di valori rappresentabili in sistema binario si ottiene elevando il numero di valori assegnabili a ciascuna posizione (due, ovvero “0” e “1” che corrispondono a un circuito aperto o chiuso) per il numero di “posizioni” (i bit, appunto) disponibili.
La trasformazione del valore di tensione misurato in valore digitale, la quantizzazione, avviene a cura del circuito di Quantize all’interno del quale il valore di tensione viene approssimato al più vicino dei valori disponibili, a seconda quindi della risoluzione in bit alla quale avviene il processo di conversione. Sempre semplificando un tantino, le immagini successive vi mostrano la stessa sine wave di poco fa con la sovrapposizione di una serie di informazioni:
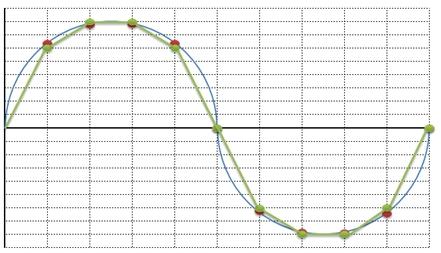
a) Sovrapposta in verde, la ricostruzione dell’onda di cui sopra, dopo il processo di approssimazione ai valori disponibili (linee tratteggiate orizzontali) negli istanti in cui avviene il campionamento (linee tratteggiate verticali).
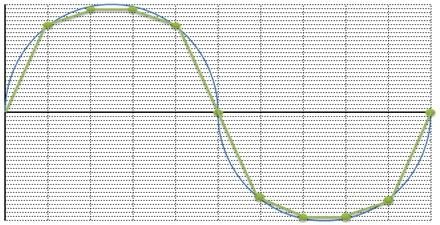
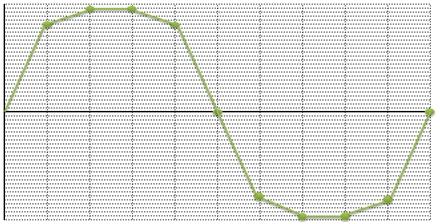
b) La stessa sine wave campionata alla stessa frequenza, a una risoluzione tripla rispetto alla precedente. Aumenta la densità delle linee orizzontali, quindi migliora l’approssimazione dei valori assegnati, rispetto ai valori di tensione originari
c) La stessa onda ricostruita, dove si nota una maggior aderenza alla “vecchia” sine wave, paragonata a quella della figura a.
La differenza tra il valore di tensione misurato e il valore attribuito al campione durante il processo di quantizzazione viene appunto definito “errore di quantizzazione”. La risoluzione che scegliamo ha impatto ovviamente sul “rapporto segnale rumore” all’interno del circuito ADC, come ovviamente il range dinamico sfruttabile all’interno del circuito (che in un circuito ADC viene definito SQNR, signal to quantizazion noise ratio) che, idealmente e senza stare troppo a incasinarci con i numeri, si calcola moltiplicando per 6 il numero di bit di quantizzazione. A 16 bit, SQNR corrisponde a circa 96 dB mentre a 24 bit il range teorico aumenta a 144 dB che incorpora abbondantemente i limiti delle capacità uditive dell’essere umano. In ogni caso, ho scoperto in una mia lettura recente che è pressoché universalmente riconosciuto un massimo SNR pari a poco più di 120 dB (attorno ai 21 bit) a causa dei vincoli costruttivi nella progettazione dei circuiti integrati moderni.
La scelta ottimale sarebbe quella di optare, sempre, per la maggior risoluzione possibile. Di contro però questa scelta fa i conti con la necessità di lavorare con file di dimensioni maggiori, con aggravio di costi (pur oggigiorno meno importanti rispetto a solamente un lustro fa…) per maggiori prestazioni, spazio di archiviazione, ecc.
Per rendere meglio l’idea, la regola per calcolare le dimensioni di un file audio è molto semplice: questa è data dal prodotto di risoluzione in bit, frequenza di campionamento in Hz, numero di canali (ovviamente un file mono avrà un peso, un file stereo con le stesse caratteristiche peserà il doppio) e lunghezza – durata in secondi – del file), ovvero:
Dimensioni file audio in bit = no. bit X freq. di camp. in Herz X durata in secondi X numero canali
Un file Wave stereo a 16 bit 44,1 KHz (le caratteristiche dei file audio stampati su CD audio) di 4 minuti peserà quindi:
16 X 44.100 X 240 X 2 = 338.688.000 bit, pari a 40,37 Mb ( 1 Mb = 8.388.608 bit).
Lo stesso file, con stessa frequenza di campionamento, ma risoluzione pari a 24 bit peserà invece:
24 X 44.100 X 240 X 2 = 508.032.000 bit, pari a 60,56 Mb
Sul singolo file ovviamente la differenza è poco significativa, moltiplicatela però per tutti i file audio che acquisite durante una registrazione di un brano e potete capire come, seppur oggi la registrazione a 24 bit sia più che consolidata (io stesso, in registrazione, non riprendo mai sotto i 24 bit con frequenza di campionamento a 48 KHz), anche solo pochi anni fa la diversa richiesta di spazio di archiviazione era dirimente sulla scelta della risoluzione del progetto.
Sorgente: Accordo: Campionamento e Quantizzazione